基于小波变换的模糊图像融合算法matlab仿真

目录
小波分析是当前应用数学和工程学科中一个迅速发展的新领域,经过近10年的探索研究,重要的数学形式化体系已经建立,理论基础更加扎实。与Fourier变换相比,小波变换是空间(时间)和频率的局部变换,因而能有效地从信号中提取信息。通过伸缩和平移等运算功能可对函数或信号进行多尺度的细化分析,解决了Fourier变换不能解决的许多困难问题。
基于小波变换的模糊图像融合算法是一种有效的图像处理技术,它结合了小波变换的多尺度分析和图像融合的思想,旨在从多个源图像中提取并融合重要信息,以生成一幅包含各源图像显著特征的高质量图像。图像融合(Image Fusion)是指将多源信道所采集到的关于同一目标的图像数据经过图像处理和计算机技术等,最大限度的提取各自信道中的有利信息,最后综合成高质量的图像,以提高图像信息的利用率、改善计算机解译精度和可靠性、提升原始图像的空间分辨率和光谱分辨率,利于监测。
1. 图像的小波变换
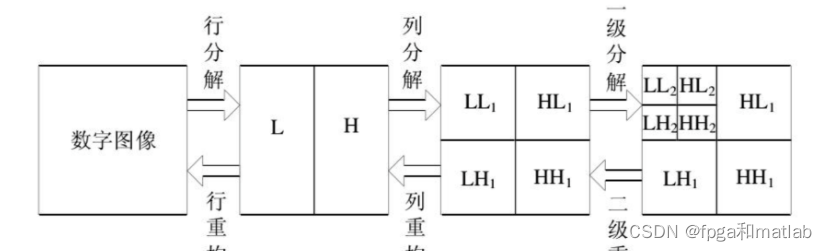
图像的二维离散小波分解和重构过程如下图所示,分解过程可描述为:首先对图像的每一行进行 1D-DWT,获得原始图像在水平方向上的低频分量 L 和高频分量 H,然后对变换所得数据的每一列进行 1D-DWT,获得原始图像在水平和垂直方向上的低频分量 LL、水平方向上的低频和垂直方向上的高频 LH、水平方向上的高频和垂直方向上的低频 HL 以及水平和垂直方向上的的高频分量 HH。
重构过程可描述为:首先对变换结果的每一列进行以为离散小波逆变换,再对变换所得数据的每一行进行一维离散小波逆变换,即可获得重构图像。由上述过程可以看出,图像的小波分解是一个将信号按照低频和有向高频进行分离的过程,分解过程中还可以根据需要对得到的 LL 分量进行进一步的小波分解,直至达到要求。
目前,图像的融合有如下几个方面的规则:
规则一:系数绝对值较大法
该融合规则适合高频成分比较丰富,亮度、对比度比较高的源图像,否则在融合图像中只保留一幅源图像的特征,其他的特征被覆盖。小波变换的实际作用是对信号解相关,并将信号的全部信息集中到一部分具有大幅值的小波系数中。这些大的小波系数含有的能量远比小系数含有的能量大,从而在信号的重构中,大的系数比小的系数更重要。
规则二:加权平均法
权重系数可调,适用范围广,可消除部分噪声,源图像信息损失较少,但会造成图像对比度的下降,需要增强图像灰度。
规则三:局部方差准则
设A(x,y)和B(x,y)分别为高频子图像数据值,F(x,y)为相应高频子图像融合值,将A(x,y)和B(x,y)分成若干个M×N子块图像。对每个子块图像进行数值分布统计,计算其方差。确定A和B图像每个子块图像加权系数K1和K2。如果A图像子块方差大于B图像子块方差,则K1≥K2,否则K1<K2。确定每个子块图像的数据融合数值为:F(i,j)=K1A(i,j)+K2B(i,j)。
下面对这几个方法进行介绍。
2. 小波变换低频LL/高频HH取绝对值较大融合
在这种融合策略中,首先对每幅源图像进行小波分解,得到低频(近似)和高频(细节)系数。低频系数反映了图像的总体信息,而高频系数则包含了图像的细节信息。
对于低频系数,取绝对值较大的系数作为融合后的低频系数。这种选择基于这样的假设:绝对值较大的低频系数包含更多的能量和信息。
对于高频系数,同样采用取绝对值较大的策略。这种选择有助于保留源图像中的显著边缘和纹理信息。
这个部分对应matlab如下:
for i=1:row
for j=1:col
if abs(c1(i,j))>abs(c2(i,j))
c(i,j)=c1(i,j);
else
c(i,j)=c2(i,j);
end
end
end3. 低频系数加权,高频绝对值较大融合
在这种策略中,低频系数采用加权平均的方式进行融合,而高频系数仍然采用取绝对值较大的策略。低频系数采用加权平均,可以根据源图像的质量、对比度等因素分配不同的权重。高频系数的融合规则与第一种策略相同,即取绝对值较大的高频系数。
这个部分对应matlab如下:
for i=1:row
for j=1:col
ca(i,j)=(ca1(i,j)+ca2(i,j))/2;
if abs(ch1(i,j))>abs(ch2(i,j))
ch(i,j)=ch1(i,j);
else
ch(i,j)=ch2(i,j);
end
if abs(cv1(i,j))>abs(cv2(i,j))
cv(i,j)=cv1(i,j);
else
cv(i,j)=cv2(i,j);
end
if abs(cd1(i,j))>abs(cd2(i,j))
cd(i,j)=cd1(i,j);
else
cd(i,j)=cd2(i,j);
end
end
end4. 低频小波系数绝对值较大融合策略,高频局部显著性融合
在这种策略中,低频系数采用取绝对值较大的方式进行融合,而高频系数则采用基于局部显著性的融合方法。低频系数的融合规则与第一种策略相同,即取绝对值较大的低频系数。对于高频系数,首先计算每个源图像的局部显著性图(可以是基于梯度、对比度或其他特征的显著性图)。然后根据显著性图来决定每个像素点的高频系数取值。
这个部分对应matlab如下:
for i=1:row
for j=1:col
%-----低频融合策略 -----%
%低频取平均
% ca(i,j)=(ca1(i,j)+ca2(i,j))/2;
%低频取绝对值大
if abs(ca1(i,j))>abs(ca2(i,j))
ca(i,j)=ca1(i,j);
else
ca(i,j)=ca2(i,j);
end
%-----高频融合策略 -----%
if sh1(i,j)>=sh2(i,j)
mhx(i,j)=1;
mhy(i,j)=0;
else
mhx(i,j)=0;
mhy(i,j)=1;
end
if sv1(i,j)>=sv2(i,j)
mvx(i,j)=1;
mvy(i,j)=0;
else
mvx(i,j)=0;
mvy(i,j)=1;
end
if sd1(i,j)>=sd2(i,j)
md(i,j)=1;
md(i,j)=0;
else
md(i,j)=0;
md(i,j)=1;
end
end
end
fun2 = inline('sum(x(:))')
mxx=nlfilter(mhx,[3 3],fun2);
mvv=nlfilter(mvx,[3 3],fun2);
mdd=nlfilter(mhx,[3 3],fun2);
for i=1:row
for j=1:col
if mxx(i,j)>=5
ch(i,j)=ch1(i,j);
else
ch(i,j)=ch2(i,j);
end
if mvv(i,j)>=5
cv(i,j)=cv1(i,j);
else
cv(i,j)=cv2(i,j);
end
if mdd(i,j)>=5
cd(i,j)=cd1(i,j);
else
cd(i,j)=cd2(i,j);
end
end
end基于小波变换的模糊图像融合算法通过在不同频率子带上应用不同的融合规则,能够有效地从多个源图像中提取并融合重要信息。上述三种融合策略各有特点,可以根据具体应用场景和需求选择合适的策略。在实际应用中,还可以结合其他图像处理技术(如图像增强、去噪等)来进一步提高融合图像的质量。
5. matlab程序和测试结果
clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
rng('default')
x1=imread('1.bmp');
x2=imread('2.bmp');
%拼接融合
A=func_fusion1(x1,x2);
%小波变换低频\高频取绝对值较大融合
B=func_fusion2(x1,x2);
%低频系数加权,高频绝对值较大融合
C=func_fusion2(x1,x2);
%低频小波系数绝对值较大融合策略,高频局部显著性融合
D=func_fusion4(x1,x2);
figure;
subplot(2,4,[1,2]);imshow(x1)
subplot(2,4,[3,4]);imshow(x2)
subplot(2,4,5);imshow(A);title('拼接融合');
subplot(2,4,6);imshow(B);title('小波变换低频\高频取绝对值较大融合');
subplot(2,4,7);imshow(C);title('低频系数加权,高频绝对值较大融合');
subplot(2,4,8);imshow(D);title('低频小波系数绝对值较大融合策略,高频局部显著性融合');
测试结果如下:

